Fundamentos de Biomecánica – Parte 1

Ing. Raúl J. Amil

    La presente nota es la primera de una serie que tiene por objeto difundir entre los interesados los conceptos básicos de la Biomecánica Deportiva y los fundamentos físicos y matemáticos que permiten su análisis y comprensión.

1.1. Introducción
   La etimología del término Biomecánica proviene de las palabras Biología, ciencia que estudia los seres vivos, y Mecánica, rama de la Física que estudia el movimiento de los cuerpos. Por lo tanto se define a la Biomecánica como la ciencia que estudia la estructura y función de los sistemas biológicos aplicando las leyes de la mecánica.
   Cuando el estudio se circunscribe al análisis de los movimientos dentro de la actividad física y el deporte se suele hablar de Biomecánica Deportiva.
   Quizás el aporte más interesante de la Biomecánica es que permite abordar desde una perspectiva científica el análisis del gesto deportivo, posibilitando así perfeccionar la técnica. Justamente se la puede definir como ciencia debido a que aplica el Método Científico, el cual según el filósofo y físico argentino Mario Bunge (1), se lo puede sintetizar como el procedimiento regular, explícito y repetible mediante el cual se alcanza un objetivo.

1.2. Divisiones de la Mecánica: Dinámica y Estática
   La Dinámica es la rama de la Mecánica que estudia el movimiento de los cuerpos bajo la acción de las fuerzas, mientras que a Estática es la encargada del estudio de la acción de las fuerzas sobre los cuerpos en reposo o en equilibrio.
   A su vez la Dinámica está constituida en dos partes: la Cinemática, que es el estudio del movimiento sin hacer referencia a las fuerzas que lo originan, y la Cinética, que relaciona la acción de las fuerzas que se ejercen sobre los cuerpos con los movimientos resultantes.
   Así por ejemplo cuando se determina la fuerza que ejerce contra el suelo la pierna de pique de un saltador, y como se relaciona esto con la altura obtenida en el salto, estamos ante un problema dinámico. Si en cambio, nos interesa la velocidad, la altura, el ángulo de salida, y la distancia que alcanzará la bala cuando estudiamos a un lanzador, nos encontramos con un problema cinemático, mientras que si estudiamos la magnitud dirección y sentido de las fuerzas que determinan la posición de equilibrio de un gimnasta cuando realiza un "Cristo" en las anillas, el análisis del problema es territorio de la Estática.

1.3. Medidas y sistemas de unidades
   Sin duda ciertas apreciaciones cualitativas sirven para tener una comprensión de ciertos fenómenos de la naturaleza. Sin embargo cuando dicha apreciación pretende ser precisa e independiente de quien la formula, debe ser expresada en lenguaje matemático. Por ejemplo si decimos que un atleta es veloz, por la simple observación de la rapidez con que ejecuta el gesto deportivo, estamos ante una apreciación relativa al observador. En cambio si expresamos que dicho atleta es capaz de recorrer los 100m llanos a una velocidad media de 10 m/s, la apreciación pierde su relatividad, ya que hemos medido su velocidad relacionando dos patrones estándar como distancia y tiempo. Como corolario podemos enunciar que medir es comparar una magnitud con otra denominada patrón, cuya característica fundamental es la invariabilidad.
   En Biomecánica se utilizan magnitudes físicas denominadas arbitrariamente fundamentales, como la Longitud (L), la Masa (M), y el Tiempo (T). El resto de las magnitudes, llamadas derivadas, como la fuerza o la aceleración, se obtienen relacionando matemáticamente las anteriores. Estas magnitudes se deben expresar en una determinada unidad de medida, y la selección de estas unidades estándar se denomina Sistema de Unidades. En adelante adoptaremos el Sistema Internacional, que utiliza para la Longitud el metro, para la Masa el kilogramo, y para el Tiempo el segundo.

1.4. Sistemas de referencia
   En general, el valor que se mide de una cantidad física depende del marco de referencia del observador que efectúa la medición. Por ejemplo, la velocidad de un bote de remo tendrá un cierto valor para un observador situado en la costa, otra para un competidor situado en otro bote y desplazándose a una velocidad diferente del anterior, y nula si la mide el remero que conduce el bote de referencia.
   En Biomecánica se emplearán los llamados Sistemas de referencia inerciales, los cuales se consideran no acelerados y no giratorios, y que se mueven con velocidad uniforme, unos con respecto a otros y con respecto a las estrellas fijas. La experiencia confirma que todos los sistemas de referencia inerciales son equivalentes para la medición de los fenómenos físicos. Los observadores situados en diferentes sistemas pueden obtener diferentes valores numéricos de las cantidades físicas medidas, pero las relaciones entre dichas cantidades, esto es, las leyes de la Física, serán las mismas para todos los observadores

1.5. Funciones trigonométricas
   Las funciones trigonométricas nos permiten relacionar los ángulos y lados de los triángulos rectángulos.
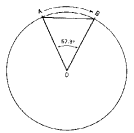
   Usualmente los ángulos se miden en grados (º), que es el ángulo que resulta de dividir una circunferencia en 360 partes iguales, o bien en radianes. Un radián (rad) es un ángulo cuya longitud de arco es igual al radio de la circunferencia, y equivale a 57.3º (Fig. 1)

Figura 1: representación de un radián Figura

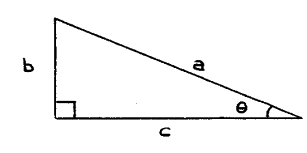
2: triángulo rectángulo

   La Fig. 2 nos muestra un triángulo rectángulo de catetos b y c, e hipotenusa a. Las funciones trigonométricas seno, coseno y tangente se obtienen de relacionar los lados en la siguiente forma:

Sen q = cateto opuesto/hipotenusa = b/a

Cos q = cateto adyacente/hipotenusa = c/a

Tan q = cateto opuesto/cateto adyacente = b/c

    Por otra parte, el Teorema de Pitágoras expresa la relación entre los catetos y la hipotenusa de triángulo rectángulo:

a² = b² + c²

1.6. Cálculo diferencial

1.6.1. Funciones
   Si a cada uno de los valores que puede tomar una magnitud variable x, perteneciente a un determinado conjunto E, corresponde un valor único, finito y determinado de magnitud y, dicha magnitud recibe el nombre de función de x determinada en el conjunto E.

La notación abreviada de dicha función es: y = f(x)

A y se la suele llamar variable dependiente, y a x variable independiente

Al conjunto de valores de x que determinan la función dada se lo denomina campo de existencia de la función.

1.6.2. Derivadas
   Sea una función cualquiera y = f(x), tal que para un valor de x = x₁, y toma un valor y₁, y para otro valor x=x₂, y toma un valor y₂. Al incremento de x se lo llama D x y es igual a x₂-x₁, y el correspondiente a y se denomina D y, tal que D y = y₂-y_1.

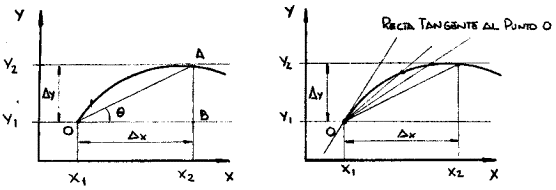
Figura 3a Figura 3b

    Si consideramos a D x y a D y como los lados de un triángulo rectángulo OAB (Figura 3a), la tangente trigonométrica del ángulo q resultará: tgq = D y/D x, que también representa la pendiente de la recta OA.

    Si hacemos cada vez más pequeño el incremento de D x, (Figura 3b), hasta que dicho valor tienda a cero (D x 0), el punto A tiende a lo largo de la curva hacia el punto O, y la recta que pasa por OA tiende a convertirse en la recta tangente a la curva en el punto O (x₁, y₁).

    La pendiente de esta recta tangente es la derivada de y con respecto a x, y se escribe:

Lim D y / D x = dy/dx

D x 0

    Las derivadas tienen gran aplicación en el campo de la Biomecánica Deportiva. Por ejemplo como veremos luego, la derivada del desplazamiento es la velocidad, y la de la velocidad es la aceleración.

1.7. Cálculo integral
   La operación inversa a la derivación es la denominada integración.

Sea una función y = f(x) (Figura 4), definida en un segmento a < x < b, consideremos una división arbitraria de dicho segmento en n partes, tal que a = x₀<x₁<x₂< ... <x_n =b.

    Se define como suma integral de la función f(x) en el intervalo [a, b] a la expresión:

                                                                        _n-1
                                             Sn = å f(x _i). D x_i
                                                                        ⁱ⁼⁰

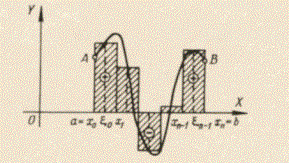Figura 4: Representación gráfica de la función y = f(x) (de "Problemas y ejercicios de análisis matemáticos de Demidovich)

    Sn representa geométricamente la suma algebraica de las áreas de los correspondientes paralelogramos. Sin embargo cuando queremos aumentar la precisión de la determinación del área bajo la curva, el número de divisiones n deberá hacerse mayor, y los incrementos D x_i deberán ser más pequeños.
    Al límite de la suma Sn cuando el número n de divisiones tiende a infinito, y el mayor de los incrementos D x_i tiende a cero, se la llama integral definida de la función f(x) entre los límites x = a, y x = b.

                                                                                                                                                                 _{n-1                         b}
                                           Lim = å f(x _i). D x_i = ò  f(x) dx
                             max D x_i   0          ^{i=0                          a}

Como ejemplo de aplicación práctica podemos decir que al ser la integración el proceso inverso a la derivación, conociendo la ecuación que determina la aceleración podemos obtener la de la velocidad, y a partir de una nueva integración, la del desplazamiento.

Bibliografía utilizada
RESNICK, R., HALLIDAY, D. Física I. Cecsa, 1978
MERIAM, J. Dinámica. Editorial Reverté, 1984
GUTIERREZ DAVILA, M. Biomecánica Deportiva. Editorial Síntesis, 1998
DEMIDOVICH, B., Problemas y Ejercicios de Análisis Matemático. Paraninfo 1982

(1) Para una descripción completa del Método Científico, véase: BUNGE, MARIO. La ciencia, su método y su filosofía. Ediciones Siglo Veinte.

Ing. Raúl J. Amil
rauljamil@hotmail.com